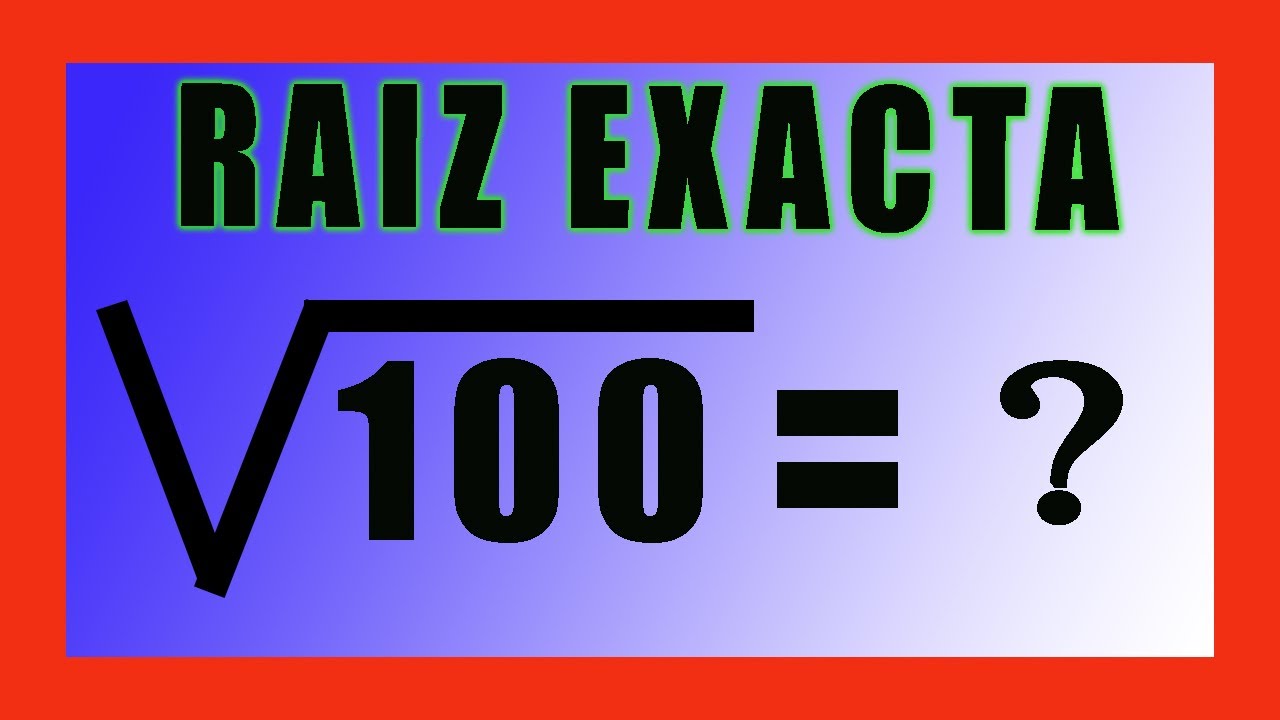Listen up, folks! If you're here, you're probably wondering, what is the square root of 100? Well, let me tell you, this ain't just a math problem—it’s a gateway to understanding some pretty cool stuff about numbers, patterns, and even the world around us. Whether you’re a student brushing up on your math skills or just someone curious about the magic of numbers, we’re diving deep into this topic. So, buckle up, because it’s gonna be a fun ride!
Now, before we get all technical, let’s take a step back. Numbers are everywhere, man. They’re in the music you listen to, the buildings you walk into, and even the pizza you devour on Friday nights. Understanding math isn’t just about solving equations—it’s about seeing how everything connects. And trust me, once you grasp the concept of square roots, you’ll start noticing them in the most unexpected places.
So, why are we talking about the square root of 100? Well, it’s not just any random number. It’s a perfect square, and perfect squares are like the rock stars of the math world. They’ve got personality, they’ve got style, and they make everything a little bit easier to understand. So, let’s break it down, piece by piece, and figure out what makes this number so special.
Table of Contents
- What is a Square Root?
- The Square Root of 100
- Perfect Squares: Why They Matter
- A Brief History of Square Roots
- Real-World Applications
- How to Calculate Square Roots
- Common Mistakes to Avoid
- Advanced Concepts in Square Roots
- Fun Facts About Square Roots
- Wrapping It Up
What is a Square Root?
Alright, let’s start with the basics. What exactly is a square root? Think of it like this: a square root is the number you multiply by itself to get another number. For example, if you multiply 5 by 5, you get 25. So, the square root of 25 is 5. Simple, right? But here’s the kicker—square roots can get a little tricky when you’re dealing with non-perfect squares. We’ll dive into that later, but for now, just remember this: square roots are all about finding the original number that, when squared, gives you the result.
Why Do We Use Square Roots?
Now, you might be thinking, “Why do we even need square roots?” Great question! Square roots are used in a ton of real-world situations. Engineers use them to calculate distances, architects rely on them to design buildings, and scientists use them to solve complex equations. Even your favorite video games use square roots to calculate distances between characters and objects on the screen. So, yeah, they’re kind of a big deal.
The Square Root of 100
Let’s get to the heart of the matter. What is the square root of 100? Drumroll, please! The answer is… 10! That’s right, folks. When you multiply 10 by 10, you get 100. And that’s why 10 is the square root of 100. But here’s where things get interesting. Did you know that 100 is a perfect square? That means it’s the result of multiplying an integer by itself. In this case, 10 × 10 = 100. Pretty neat, huh?
Why is 100 a Perfect Square?
Perfect squares are numbers that can be expressed as the product of an integer multiplied by itself. For example, 1 (1 × 1), 4 (2 × 2), 9 (3 × 3), 16 (4 × 4), and so on. 100 is special because it’s one of these perfect squares. It’s like the golden child of the math world—always well-behaved and easy to work with. But don’t let that fool you. Perfect squares have their own set of quirks and secrets, which we’ll explore in a bit.
Perfect Squares: Why They Matter
Perfect squares aren’t just cool because they’re easy to calculate. They’re also super useful in a variety of fields. For instance, they’re used in geometry to calculate areas of squares and rectangles. In physics, they help determine the speed and distance of moving objects. And in computer science, they’re used in algorithms to optimize performance. So, yeah, perfect squares are kind of a big deal.
Examples of Perfect Squares
Let’s take a look at some other perfect squares:
- 1 (1 × 1)
- 4 (2 × 2)
- 9 (3 × 3)
- 16 (4 × 4)
- 25 (5 × 5)
- 36 (6 × 6)
- 49 (7 × 7)
- 64 (8 × 8)
- 81 (9 × 9)
- 100 (10 × 10)
See the pattern? Each number is the result of multiplying an integer by itself. And that’s what makes them so special.
A Brief History of Square Roots
Believe it or not, square roots have been around for thousands of years. Ancient civilizations like the Babylonians and Egyptians were using them way back in the day. The Babylonians even had a method for approximating square roots that was surprisingly accurate for their time. And let’s not forget the Greeks, who were all about geometry and used square roots to solve problems related to shapes and areas.
How Did Square Roots Evolve?
As math evolved, so did our understanding of square roots. In the 16th century, mathematicians like René Descartes and Isaac Newton started exploring more complex concepts, like irrational numbers and square roots of negative numbers. And today, square roots are an essential part of algebra, calculus, and pretty much every branch of mathematics you can think of.
Real-World Applications
So, how does all this math stuff apply to the real world? Well, let me tell you, square roots are everywhere! Here are just a few examples:
- Engineering: Engineers use square roots to calculate distances, forces, and stresses in structures.
- Physics: Physicists use square roots to determine the speed and acceleration of objects.
- Computer Science: Programmers use square roots in algorithms to optimize performance and solve complex problems.
- Finance: Financial analysts use square roots to calculate risk and return on investments.
See? Square roots aren’t just for math geeks. They’re an essential part of everyday life, whether you realize it or not.
How to Calculate Square Roots
Now, let’s get practical. How do you actually calculate square roots? There are a few methods you can use:
- By Hand: You can use the long division method to calculate square roots manually. It’s a bit tedious, but it works!
- Using a Calculator: Most calculators have a square root function, so you can get the answer in seconds.
- Using Software: Programs like Excel and Python have built-in functions for calculating square roots, making it super easy.
Of course, if you’re dealing with perfect squares like 100, you can probably figure it out in your head. But for more complex numbers, these methods come in handy.
Common Mistakes to Avoid
Even the best of us make mistakes when working with square roots. Here are a few to watch out for:
- Forgetting the Negative Root: Every positive number has two square roots—one positive and one negative. Don’t forget to include the negative root when solving equations.
- Rounding Errors: When working with non-perfect squares, it’s easy to round off too early. Be careful with your calculations to avoid losing precision.
- Confusing Square Roots with Exponents: Square roots and exponents are related, but they’re not the same thing. Make sure you understand the difference before diving into calculations.
By avoiding these common pitfalls, you’ll be well on your way to mastering square roots.
Advanced Concepts in Square Roots
Ready to take things to the next level? Here are a few advanced concepts related to square roots:
- Irrational Numbers: Not all square roots are integers. Some, like the square root of 2, are irrational numbers that go on forever without repeating.
- Imaginary Numbers: What happens when you try to take the square root of a negative number? Enter imaginary numbers, which open up a whole new world of math.
- Applications in Calculus: Square roots are used extensively in calculus to solve problems related to rates of change and optimization.
These concepts might seem intimidating at first, but with a little practice, you’ll be tackling them like a pro.
Fun Facts About Square Roots
Before we wrap up, here are a few fun facts about square roots:
- The symbol for square root (√) is called a radical.
- The square root of 2 is often referred to as the “irrational number of the gods” because it’s so important in geometry.
- Leonhard Euler, one of the greatest mathematicians of all time, made significant contributions to the study of square roots.
See? Square roots aren’t just about numbers—they’re also about history, culture, and human curiosity.
Wrapping It Up
Well, folks, that’s the scoop on the square root of 100. From its humble beginnings as a perfect square to its widespread applications in the real world, square roots are truly fascinating. Whether you’re a math enthusiast or just someone looking to expand your knowledge, I hope this article has given you a new appreciation for these amazing numbers.
So, what’s next? Why not share this article with a friend? Or leave a comment below and let me know what you think. And if you’re hungry for more math knowledge, be sure to check out some of our other articles. Until next time, keep exploring, keep learning, and keep having fun with numbers!